
红黑树是树的数据结构中最为重要的一种。Java的容器TreeSet、TreeMap均使用红黑树实现。JDK1.8中HashMap中也加入了红黑树。C++ STL中的map和set同样使用红黑树实现。之前的文章已经详细介绍了2-3-4树的性质与操作。本篇文章将从2-3-4树与红黑树关系出发,详细阐明红黑树。 2-3-4树和红黑树是完全等价的,但是2-3-4树的编程实现相对复杂,所以一般是通过实现红黑树来实现替代2-3-4树,而红黑树也同样保证在O(logN)的时间内完成查找、插入和删除操作。
红黑树是每个节点都带有颜色属性的二叉查找树,颜色或红色或黑色。在二叉查找树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
正是红黑树的这5条性质,使一棵n个结点的红黑树始终保持了logn的高度,从而也就解释了上面所说的“红黑树的查找、插入、删除的时间复杂度最坏为O(log n)”这一结论成立的原因
通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
红黑树虽然本质上是一棵二叉查找树,但它在二叉查找树的基础上增加了着色和相关的性质使得红黑树相对平衡,从而保证了红黑树的查找、插入、删除的时间复杂度最坏为O(log n)。
如果一棵树满足红黑树,把红色节点收缩到其父节点,就变成了2-3-4树,所有红色节点都与其父节点构成3或4节点,其它节点为2节点。一颗红黑树对应唯一形态的2-3-4树,但是一颗2-3-4树可以对应多种形态的红黑树(主要是3节点可以对应两种不同的红黑树形态)。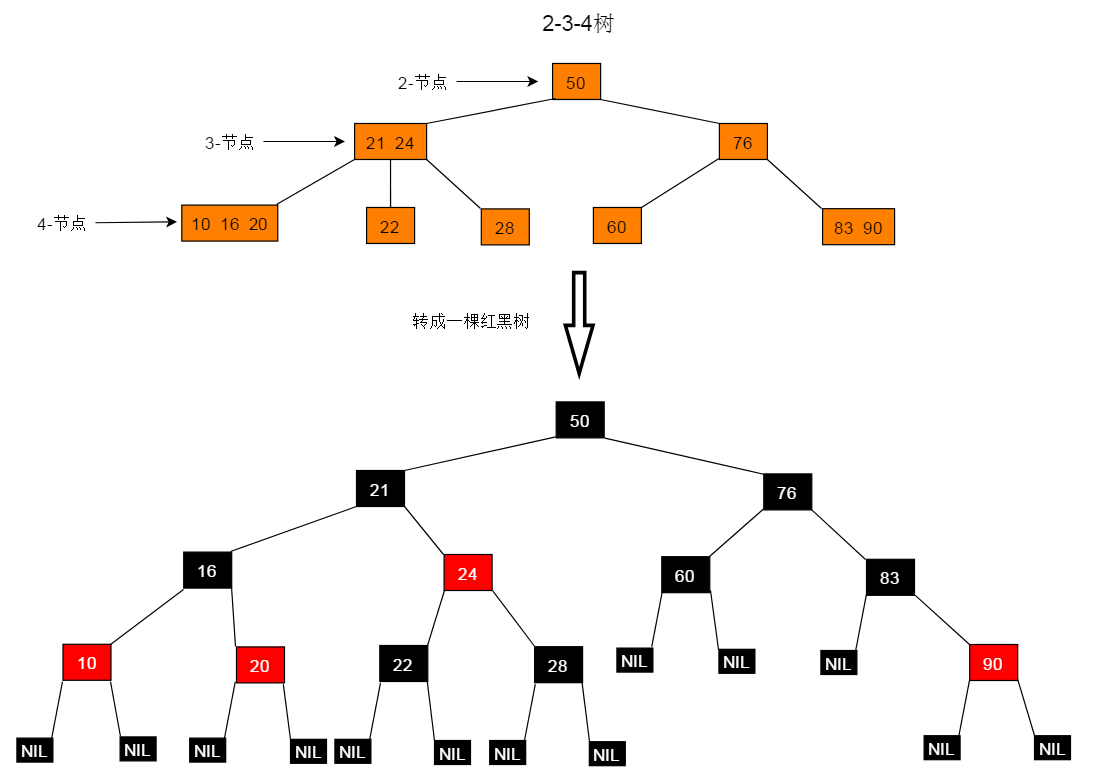
与二叉树查找一致,不再赘述
红黑树首先是一棵二叉排序树,所以它的插入操作要遵循二叉排序树的插入原则。
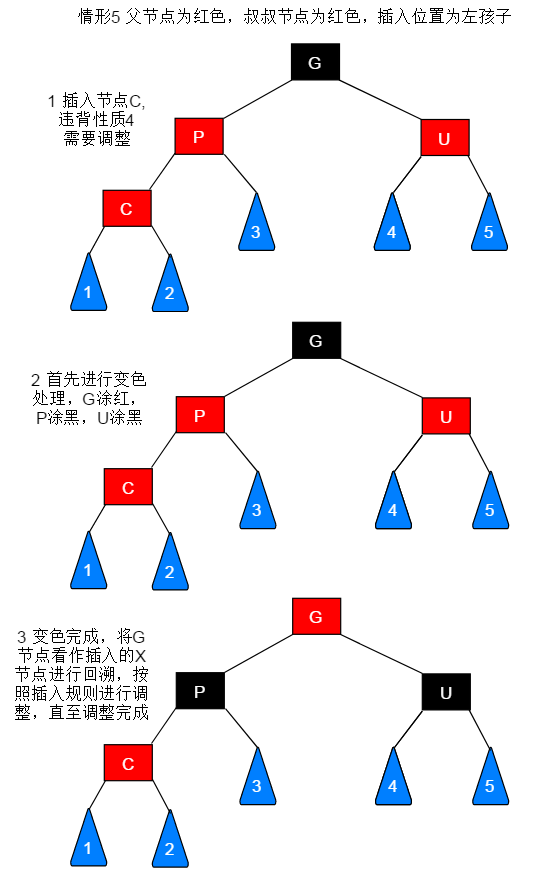
若待插入节点的父节点为红色,叔叔节点为黑色,此种情形又需要区分节点的插入位置,根据插入位置的不同进行相应的调整。此种情形共有四种:
以祖父节点(G)为中心,右旋
父节点(P)涂黑,祖父节点(G)涂红
插入结束
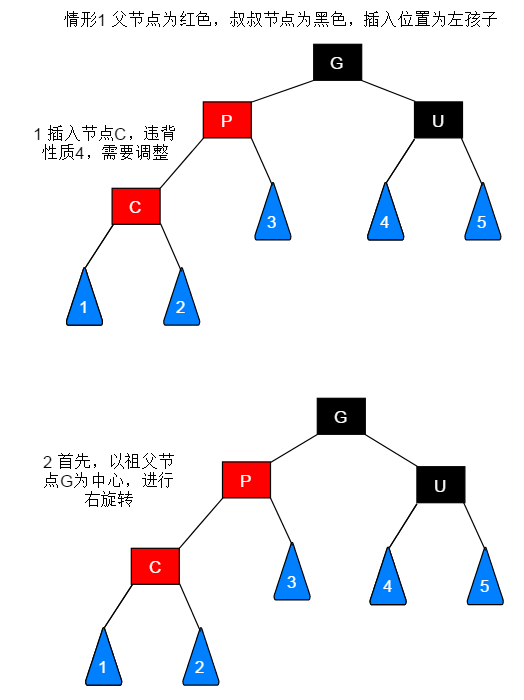
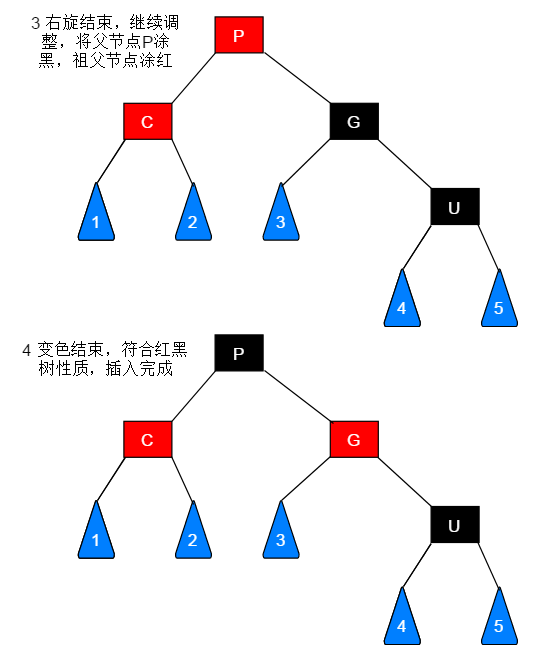
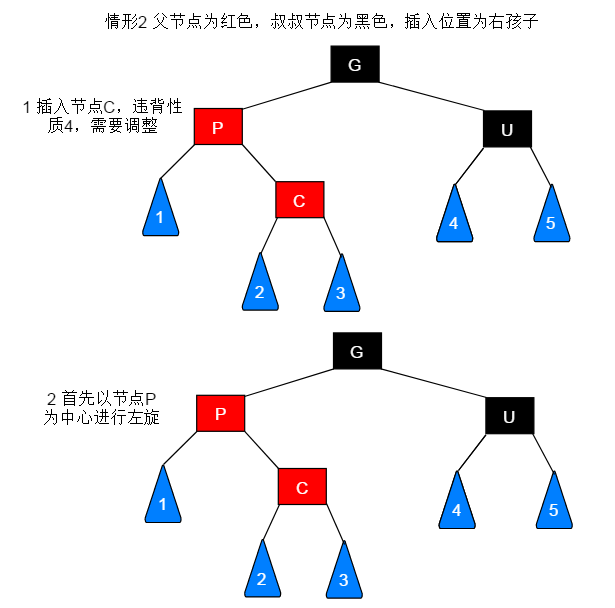
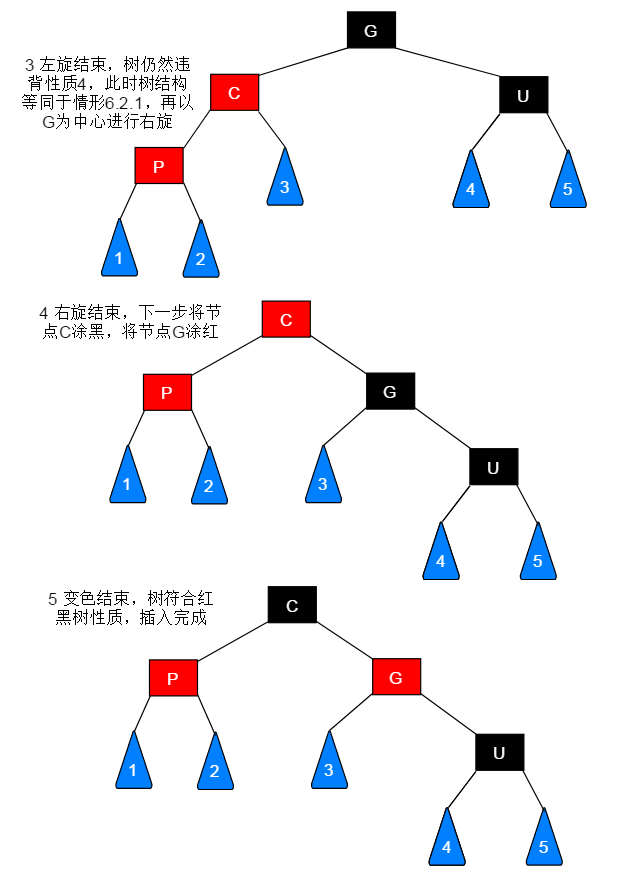
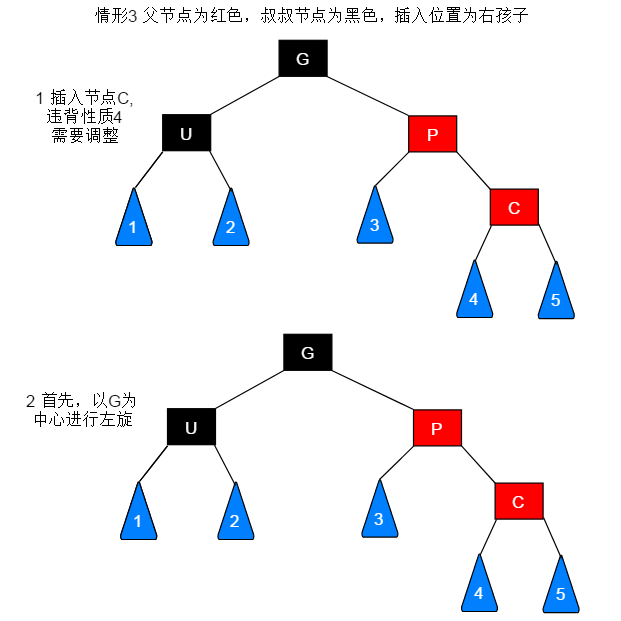
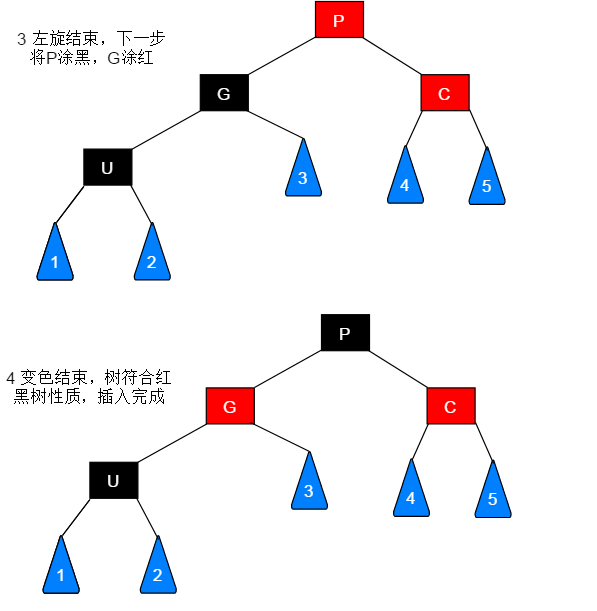
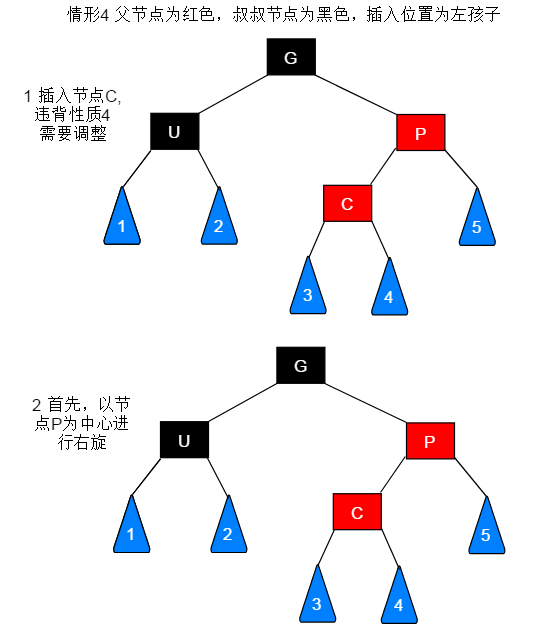
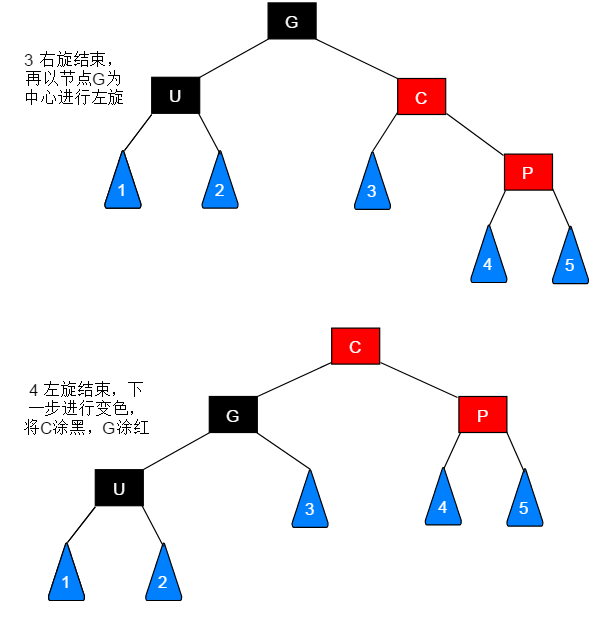
当前节点(C)为左子树或者右子树都是一套流程:
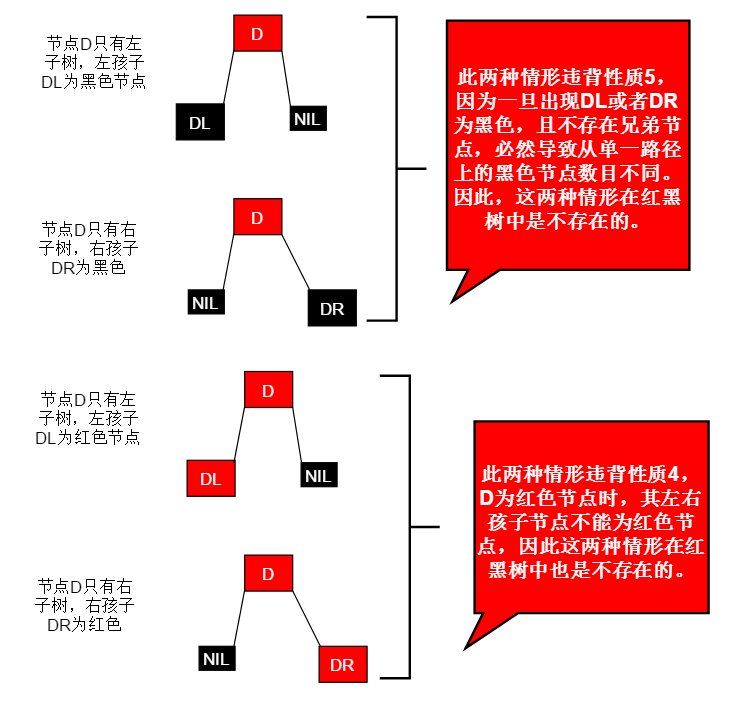
红色叶子节点(D)的父节点(P)必然是黑色,直接删除D即可
违背红黑树性质,所以不存在这种情况
用删除节点(D)的后继节点替换(只进行数据替换即可,颜色不变,此时也不需要调整结构),然后删除后继节点,后继节点的删除同样要遵循红黑树的删除过程。
不存在左(右)孩子为红色因为违背了性质5
图中填充为绿色的节点代表既可以是红色也可以是黑色,下同。
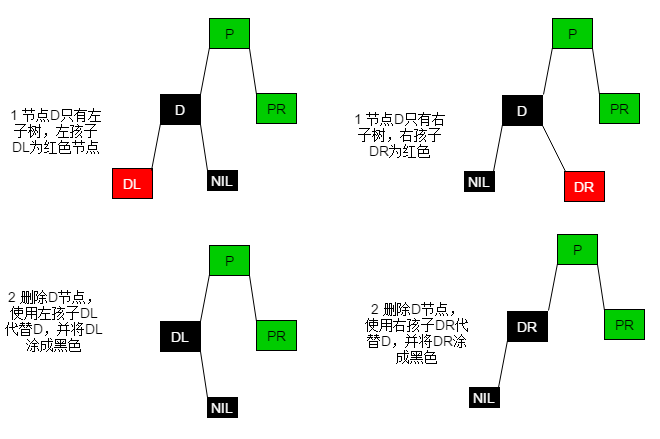
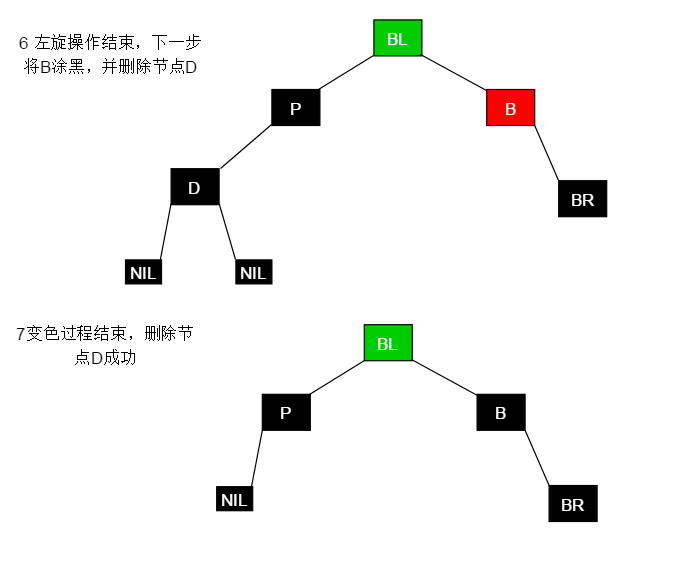
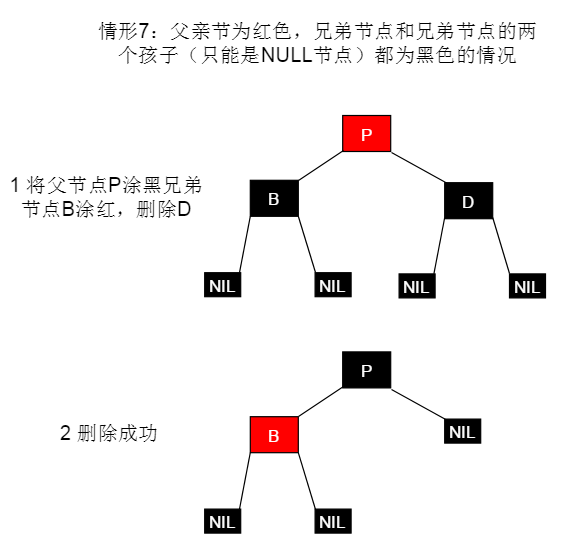
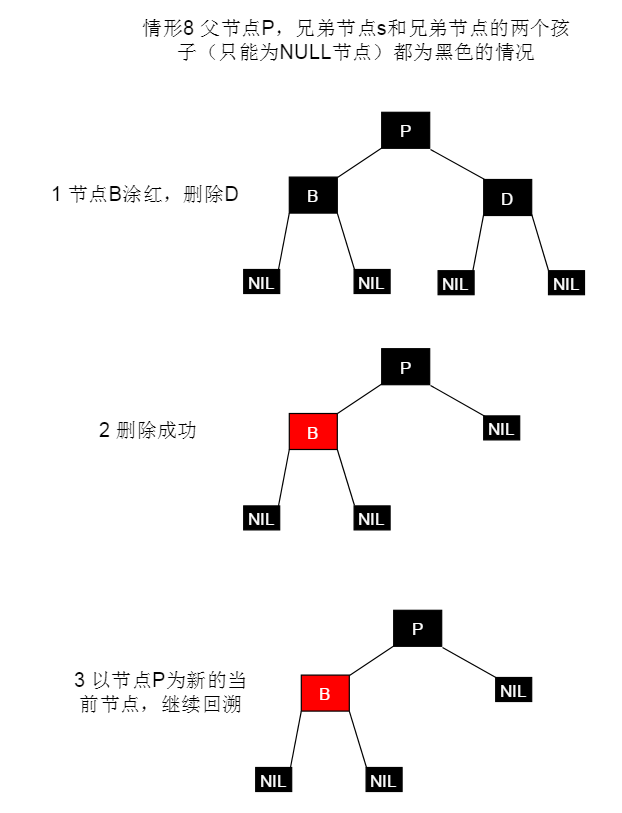
黑色叶子节点(D)的删除分为两步骤,节点调整以及删除应当先调整节点之间的关系,再执行删除操作(仅有部分情形将会结束调整,而执行删除操作)。
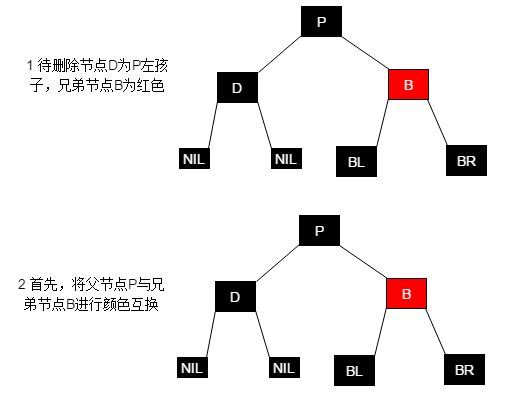
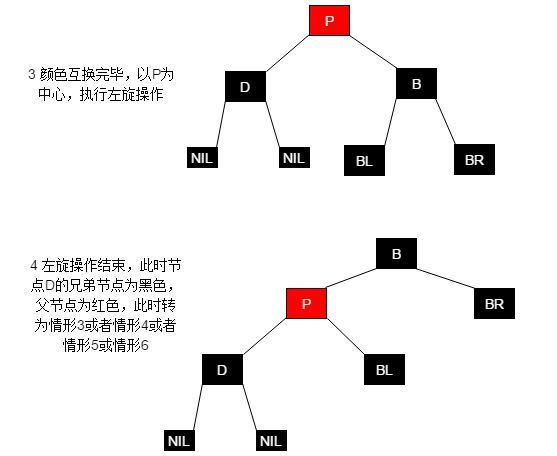
与4.5.2类似
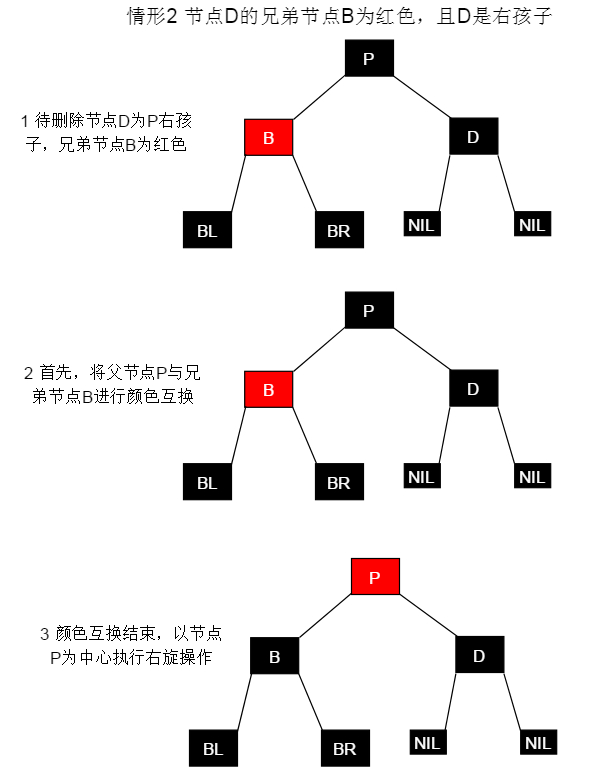
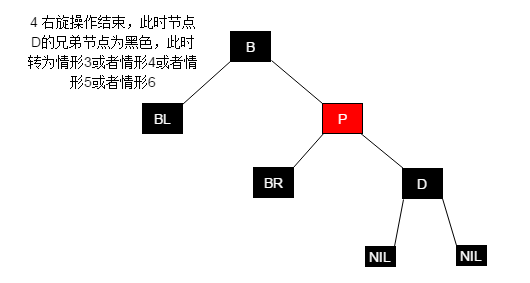
显然,这两个概念相同所以给出一份图解即可
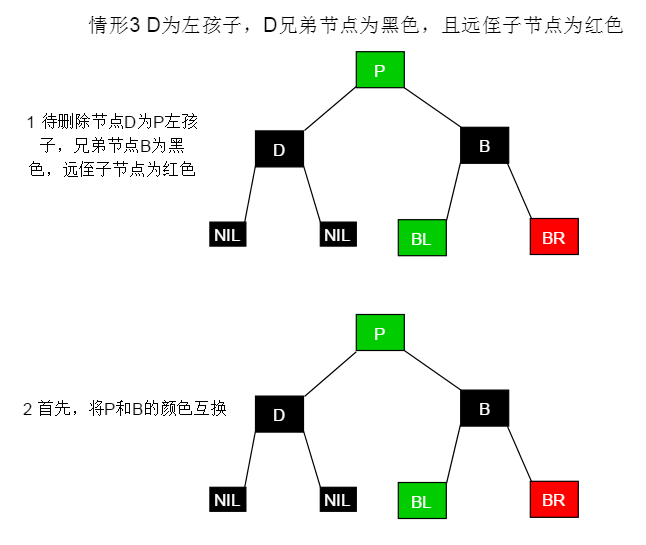
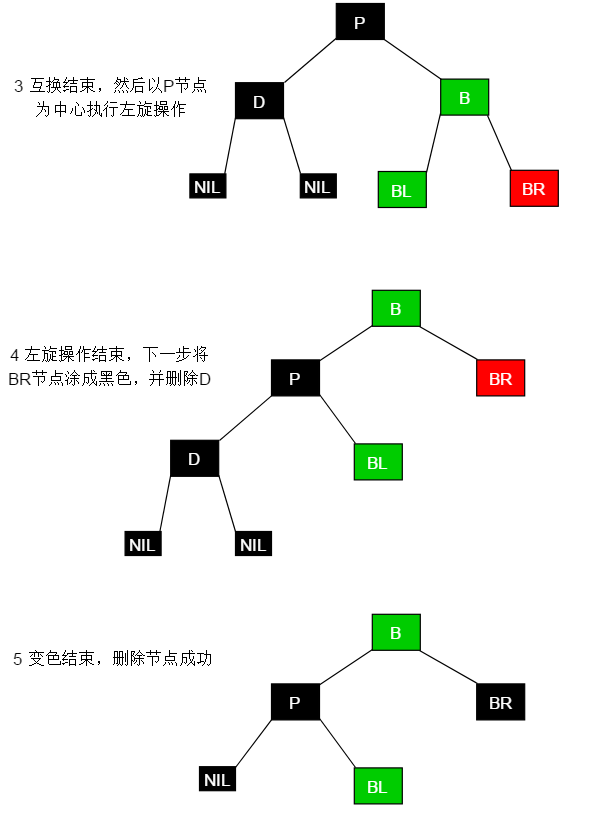
显然,这两种情形概念相同,所以给出一份图解即可
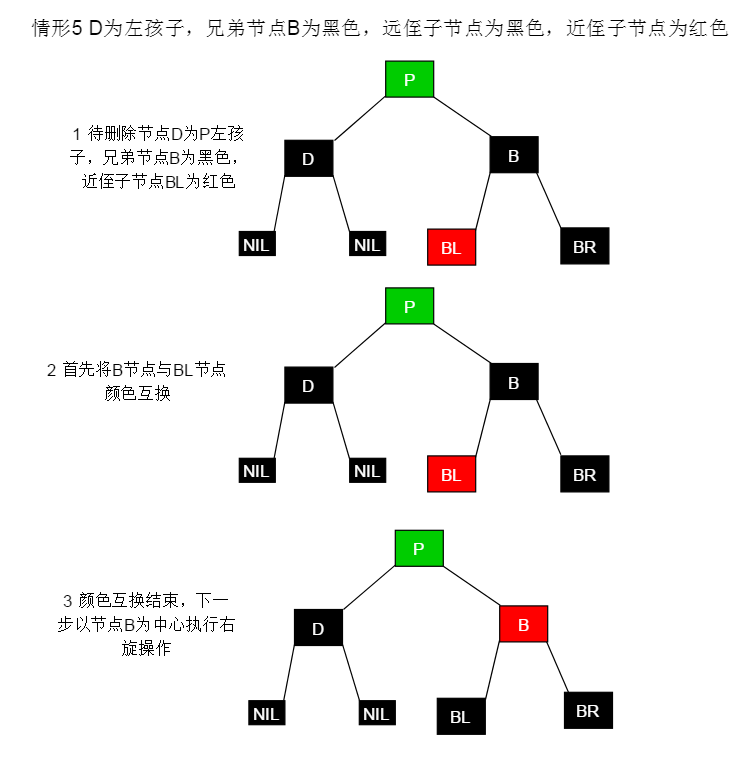
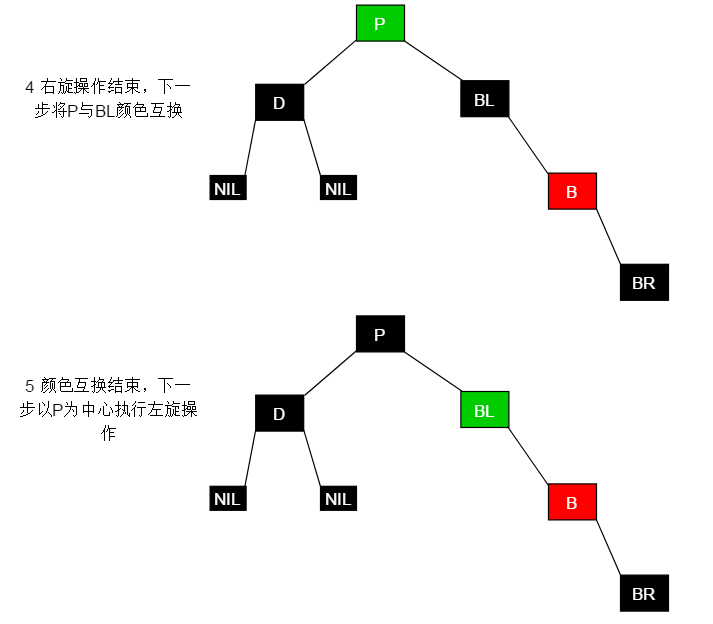
红黑树是数据结构最为重要的一种树形结构,其应用场景也是十分广泛。牢记红黑树的5条性质最为重要
package red_black_tree
import (
"errors"
"fmt"
"github.com/Ccheers/temp_test/my_data_struct_and_algorithms/tree"
"math"
"strconv"
"strings"
"sync"
)
type RedBlackFlag bool
const (
_RED RedBlackFlag = true
_BLACK RedBlackFlag = false
)
//(1)节点是要么红色或要么是黑色。
//(2)根一定是黑色节点。
//(3)每个叶子节点都带有两个空的黑色节点(称之为NIL节点,它又被称为黑哨兵)。
//(4)每个红色节点的两个子节点都是黑色(或者说从每个叶子到根的所有路径上不能有两个连续的红色节点)。
//(5)从任一节点到它所能到达得叶子节点的所有简单路径都包含相同数目的黑色节点。
type RedBlackTree struct {
root *redBlackTreeNode
}
func (t *RedBlackTree) Insert(node *redBlackTreeNode) *RedBlackTree {
if t.root == nil {
node.SetFlag(_BLACK)
node.SetIndex(tree.ROOT)
t.root = node
} else {
t.root.insert(node)
fixBalance(node)
t.root = t.root.findRoot()
}
return t
}
func (t *RedBlackTree) Search(data interface{}) (*redBlackTreeNode, error) {
node := NewRedBlackTreeNode(data)
return t.root.search(node)
}
func (t *RedBlackTree) Delete(data interface{}) error {
node := NewRedBlackTreeNode(data)
node, err := t.root.search(node)
if err != nil {
return err
}
deleteNode(node)
return nil
}
type redBlackTreeNode struct {
index tree.ChildrenIndex
depth int
parent, leftChildren, rightChildren *redBlackTreeNode //leftChild:0, rightChild:1, parent:2
flag RedBlackFlag
data interface{}
mutex sync.RWMutex
}
func (r *redBlackTreeNode) Depth() int {
return r.depth
}
func (r *redBlackTreeNode) SetDepth(depth int) {
r.depth = depth
}
func (r *redBlackTreeNode) Index() tree.ChildrenIndex {
return r.index
}
func (r *redBlackTreeNode) SetIndex(index tree.ChildrenIndex) {
r.index = index
}
func (r *redBlackTreeNode) Flag() RedBlackFlag {
return r.flag
}
func (r *redBlackTreeNode) SetFlag(flag RedBlackFlag) {
r.flag = flag
}
func (r *redBlackTreeNode) setRightChildren(node *redBlackTreeNode) *redBlackTreeNode {
r.rightChildren = node
return r
}
func (r *redBlackTreeNode) getRightChildren() *redBlackTreeNode {
return r.rightChildren
}
func (r *redBlackTreeNode) setLeftChildren(node *redBlackTreeNode) *redBlackTreeNode {
r.leftChildren = node
return r
}
func (r *redBlackTreeNode) getLeftChildren() *redBlackTreeNode {
return r.leftChildren
}
func (r *redBlackTreeNode) setParent(node *redBlackTreeNode) *redBlackTreeNode {
r.parent = node
return r
}
func (r *redBlackTreeNode) getParent() *redBlackTreeNode {
return r.parent
}
func (r *redBlackTreeNode) compare(treeNode *redBlackTreeNode) tree.CompareType {
if treeNode.data.(int) == r.data.(int) {
return tree.EQUAL
}
if treeNode.data.(int) > r.data.(int) {
return tree.GREATER
} else {
return tree.LESS
}
}
func (r *redBlackTreeNode) insert(node *redBlackTreeNode) {
//defer r.updateDepth()
switch r.compare(node) {
case tree.EQUAL:
return
case tree.GREATER:
if r.getRightChildren().data != nil {
r.getRightChildren().insert(node)
} else {
node.setParent(r)
node.SetIndex(tree.RIGHTCHILDREN)
r.setRightChildren(node)
}
default:
if r.getLeftChildren().data != nil {
r.getLeftChildren().insert(node)
} else {
node.setParent(r)
node.SetIndex(tree.LEFTCHILDREN)
r.setLeftChildren(node)
}
}
}
func (r *redBlackTreeNode) search(data *redBlackTreeNode) (*redBlackTreeNode, error) {
if r.data == nil {
return nil, errors.New("not found")
} else {
switch r.compare(data) {
case tree.EQUAL:
return r, nil
case tree.GREATER:
return r.getRightChildren().search(data)
default:
return r.getLeftChildren().search(data)
}
}
}
func deleteNode(data *redBlackTreeNode) {
switch true {
case data.Flag() == _RED && data.isLeaveNode():
//删除红色叶子节点
replace(data, &redBlackTreeNode{
flag: _BLACK,
})
case data.Flag() == _RED && data.getLeftChildren().data != nil && data.getRightChildren().data != nil:
//删除红色节点,既有左子树,又有右子树
successorNode := data.getRightChildren().findMin()
data.data = successorNode.data
deleteNode(successorNode)
case data.Flag() == _BLACK && data.getLeftChildren().data != nil && data.getRightChildren().data == nil:
//删除黑色节点只有左子树
data.getLeftChildren().SetFlag(_BLACK)
replace(data, data.getLeftChildren())
case data.Flag() == _BLACK && data.getLeftChildren().data == nil && data.getRightChildren().data != nil:
//删除黑色节点只有右子树
data.getRightChildren().SetFlag(_BLACK)
replace(data, data.getRightChildren())
case data.Flag() == _BLACK && data.isLeaveNode():
begin := data
for begin.getParent() != nil {
brother := begin.getBrother()
parent := begin.getParent()
brotherLeftChildren := brother.getLeftChildren()
brotherRightChildren := brother.getRightChildren()
switch true {
case begin.Index() == tree.LEFTCHILDREN && brother.Flag() == _RED:
//D为左孩子 B为红色
swapFlag(parent, brother)
leftRotate(parent)
continue
case begin.Index() == tree.RIGHTCHILDREN && brother.Flag() == _RED:
//D为右孩子 B为红色
swapFlag(parent, brother)
rightRotate(parent)
continue
case begin.Index() == tree.LEFTCHILDREN && brother.Flag() == _BLACK && brotherRightChildren.Flag() == _RED:
//D为左孩子 B为黑色 远侄子节点为红色
swapFlag(parent, brother)
leftRotate(parent)
brotherRightChildren.SetFlag(_BLACK)
goto deleteNode
case begin.Index() == tree.RIGHTCHILDREN && brother.Flag() == _BLACK && brotherLeftChildren.Flag() == _RED:
//D为右孩子 B为黑色 远侄子节点为红色
swapFlag(parent, brother)
leftRotate(parent)
brotherLeftChildren.SetFlag(_BLACK)
goto deleteNode
case begin.Index() == tree.LEFTCHILDREN && brother.Flag() == _BLACK && brotherLeftChildren.Flag() == _RED && brotherRightChildren.Flag() == _BLACK:
//D为左孩子 B为黑色 BL为红色 BR为黑色
swapFlag(brother, brotherLeftChildren)
rightRotate(brother)
continue
case begin.Index() == tree.RIGHTCHILDREN && brother.Flag() == _BLACK && brotherLeftChildren.Flag() == _BLACK && brotherRightChildren.Flag() == _RED:
//D为左孩子 B为黑色 BL为黑色 BR为黑色
swapFlag(brother, brotherRightChildren)
leftRotate(brother)
continue
case parent.Flag() == _RED && brother.Flag() == _BLACK && brotherRightChildren.Flag() == _BLACK && brotherLeftChildren.Flag() == _BLACK:
//P为红色 B和B的孩子均为黑色
parent.SetFlag(_BLACK)
brother.SetFlag(_RED)
goto deleteNode
case parent.Flag() == _BLACK && brother.Flag() == _BLACK && brotherRightChildren.Flag() == _BLACK && brotherLeftChildren.Flag() == _BLACK:
brother.SetFlag(_RED)
begin = parent
}
}
deleteNode:
replace(data, &redBlackTreeNode{
flag: _BLACK,
})
}
}
func (r *redBlackTreeNode) isLeaveNode() bool {
return r.getLeftChildren().data == nil && r.getRightChildren().data == nil
}
func (r *redBlackTreeNode) getBrother() *redBlackTreeNode {
if r.Index() == tree.LEFTCHILDREN {
return r.getParent().getRightChildren()
}
return r.getParent().getLeftChildren()
}
func swapFlag(node1, node2 *redBlackTreeNode) {
_f := node1.Flag()
node1.SetFlag(node2.Flag())
node2.SetFlag(_f)
}
func replace(currentNode, replaceNode *redBlackTreeNode) {
parent := currentNode.getParent()
replaceNode.setParent(parent)
if currentNode.Index() == tree.LEFTCHILDREN {
replaceNode.SetIndex(tree.LEFTCHILDREN)
parent.setLeftChildren(replaceNode)
} else {
replaceNode.SetIndex(tree.RIGHTCHILDREN)
parent.setRightChildren(replaceNode)
}
}
func (r *redBlackTreeNode) updateDepth() {
r.SetDepth(int(math.Max(float64(r.getLeftChildren().Depth()), float64(r.getRightChildren().Depth()))) + 1)
}
func (r *redBlackTreeNode) findRoot() *redBlackTreeNode {
if r.parent != nil {
return r.parent.findRoot()
}
return r
}
func fixBalance(treeNode *redBlackTreeNode) {
//一般情况:插入的父节点为黑色:
//将插入的节点涂红
parent := treeNode.getParent()
if parent == nil {
treeNode.SetFlag(_BLACK)
return
}
treeNode.SetFlag(_RED)
if parentFlag := parent.Flag(); parentFlag == _RED { //父节点是红色
grandPa := parent.getParent()
var uncle *redBlackTreeNode
if parent.Index() == tree.LEFTCHILDREN {
uncle = grandPa.getRightChildren()
} else {
uncle = grandPa.getLeftChildren()
}
if uncleFlag := uncle.Flag(); uncleFlag == _BLACK {
//插入节点为红色 , 叔叔节点为黑色
switch true {
case parent.Index() == tree.LEFTCHILDREN && treeNode.Index() == tree.LEFTCHILDREN:
rightRotate(grandPa)
parent.SetFlag(_BLACK)
grandPa.SetFlag(_RED)
case parent.Index() == tree.LEFTCHILDREN && treeNode.Index() == tree.RIGHTCHILDREN:
leftRotate(parent)
rightRotate(grandPa)
treeNode.SetFlag(_BLACK)
grandPa.SetFlag(_RED)
case parent.Index() == tree.RIGHTCHILDREN && treeNode.Index() == tree.RIGHTCHILDREN:
leftRotate(grandPa)
parent.SetFlag(_BLACK)
grandPa.SetFlag(_RED)
case parent.Index() == tree.RIGHTCHILDREN && treeNode.Index() == tree.LEFTCHILDREN:
rightRotate(parent)
leftRotate(grandPa)
treeNode.SetFlag(_BLACK)
grandPa.SetFlag(_RED)
}
} else { //插入节点父节点为红色 , 叔叔节点为红色
switch true {
case treeNode.Index() == tree.LEFTCHILDREN:
grandPa.SetFlag(_RED)
parent.SetFlag(_BLACK)
uncle.SetFlag(_BLACK)
fixBalance(grandPa)
case treeNode.Index() == tree.RIGHTCHILDREN:
grandPa.SetFlag(_RED)
parent.SetFlag(_BLACK)
uncle.SetFlag(_BLACK)
fixBalance(grandPa)
}
}
}
}
func NewRedBlackTreeNode(data interface{}) *redBlackTreeNode {
node := &redBlackTreeNode{
parent: nil,
leftChildren: &redBlackTreeNode{
flag: _BLACK,
},
rightChildren: &redBlackTreeNode{
flag: _BLACK,
},
flag: _RED,
data: data,
}
node.leftChildren.setParent(node)
node.rightChildren.setParent(node)
return node
}
func NewRedBlackTree() *RedBlackTree {
return new(RedBlackTree)
}
func rightRotate(node *redBlackTreeNode) {
parent, leftChildren := node.getParent(), node.getLeftChildren()
//defer leftChildren.updateDepth()
//defer node.updateDepth()
sonRightChildren := leftChildren.getRightChildren()
if parent != nil {
if node.Index() == tree.RIGHTCHILDREN {
parent.setRightChildren(leftChildren)
} else {
parent.setLeftChildren(leftChildren)
}
}
leftChildren.SetIndex(node.Index())
node.SetIndex(tree.RIGHTCHILDREN)
leftChildren.setRightChildren(node)
leftChildren.setParent(node.getParent())
node.setParent(leftChildren)
sonRightChildren.SetIndex(tree.LEFTCHILDREN)
node.setLeftChildren(sonRightChildren)
sonRightChildren.setParent(node)
}
func leftRotate(node *redBlackTreeNode) {
parent, rightChildren := node.getParent(), node.getRightChildren()
//defer rightChildren.updateDepth()
//defer node.updateDepth()
sonLeftChildren := rightChildren.getLeftChildren()
if parent != nil {
if node.Index() == tree.RIGHTCHILDREN {
parent.setRightChildren(rightChildren)
} else {
parent.setLeftChildren(rightChildren)
}
}
rightChildren.SetIndex(node.Index())
node.SetIndex(tree.LEFTCHILDREN)
rightChildren.setLeftChildren(node)
rightChildren.setParent(node.getParent())
node.setParent(rightChildren)
sonLeftChildren.SetIndex(tree.RIGHTCHILDREN)
node.setRightChildren(sonLeftChildren)
sonLeftChildren.setParent(node)
}
//打印二叉树
func PrintTree(head *redBlackTreeNode, height int, to string, length int) {
if head.data == nil {
return
}
PrintTree(head.rightChildren, height+1, "right", length)
val := to + "\"" + strconv.Itoa(head.data.(int)) + "\""
if to == "right" {
val = "⬇️" + val
} else if to == "left" {
val = "⬆️" + val
}
if head.Flag() == _BLACK {
val = val + "black"
} else {
val = val + "red"
}
lenM := len([]rune(val))
lenL := (length - lenM) / 2
lenR := length - lenM - lenL
val = GetSpace(lenL, length, head) + val + GetSpace(lenR, length, head)
fmt.Println(GetSpace(height*length, length, head), val)
PrintTree(head.leftChildren, height+1, "left", length)
}
//空格个数
func GetSpace(num, length int, node *redBlackTreeNode) string {
space := " "
var builder strings.Builder
for i := 0; i < num; i++ {
n := num/length - i/length
ancestor := getAncestor(node, n)
if i%length == 0 && ancestor.getParent() != nil {
if ancestor.Index() == tree.RIGHTCHILDREN && node.data.(int) < ancestor.data.(int) {
fmt.Fprintf(&builder, "|")
} else if ancestor.Index() == tree.LEFTCHILDREN && node.data.(int) > ancestor.data.(int) {
fmt.Fprintf(&builder, "|")
} else {
fmt.Fprintf(&builder, space)
}
} else {
fmt.Fprintf(&builder, space)
}
}
return builder.String()
}
func getAncestor(node *redBlackTreeNode, depth int) *redBlackTreeNode {
if depth != 0 {
depth--
return getAncestor(node.getParent(), depth)
} else {
return node
}
}
func (r *redBlackTreeNode) findMin() *redBlackTreeNode {
if r.getLeftChildren().data != nil {
return r.getLeftChildren().findMin()
}
return r
}
func (r *redBlackTreeNode) findMax() *redBlackTreeNode {
if r.getRightChildren().data != nil {
return r.getRightChildren().findMax()
}
return r
}
package tree
type Tree interface {
GetRightSon() Tree
SetRightSon(treeNode Tree) Tree
GetLeftSon() Tree
SetLeftSon(treeNode Tree) Tree
GetParent() Tree
SetParent(treeNode Tree) Tree
GetData() interface{}
SetData(data interface{}) Tree
GetDepth() int
SetDepth(depth int) Tree
SetChildrenType(childrenIndex ChildrenIndex) Tree
GetChildrenType() ChildrenIndex
Insert(treeNode Tree) Tree
Search(data interface{}) (Tree, error)
Del(data interface{}) (Tree, error)
FindMin() Tree
FindMax() Tree
Compare(tree Tree) CompareType
Get(key interface{}) (interface{}, error)
Set(key, value interface{}) Tree
}
type CompareType int8 //比较类型 用于比较 node 的差异(大于,小于,等于)
type ChildrenIndex int8 //节点位于父节点的位置
type DataMap map[interface{}]interface{}
const (
EQUAL CompareType = iota //节点等于当前节点
GREATER //节点大于当前节点
LESS //节点小于当前节点
)
const (
ROOT ChildrenIndex = iota //父亲节点
LEFTCHILDREN //左孩子
RIGHTCHILDREN //右孩子
)
package red_black_tree
import (
"fmt"
"math/rand"
"testing"
)
func TestRedBlackTree_Insert(t *testing.T) {
tree := NewRedBlackTree()
for i := 1; i < 1000; i++ {
fmt.Print(i, ",")
tree = tree.Insert(NewRedBlackTreeNode(i))
}
fmt.Println()
PrintTree(tree.root, 0, "root", 10)
_, err := tree.Search(254)
if err != nil {
t.Log(err)
t.Fail()
}
}
func TestRedBlackTree_Delete(t *testing.T) {
tree := NewRedBlackTree()
for i := 1; i < 1000; i++ {
fmt.Print(i, ",")
tree = tree.Insert(NewRedBlackTreeNode(i))
}
fmt.Println()
//if err := tree.Delete(12);err != nil {
// t.Log(err)
// t.Fail()
//}
//if err := tree.Delete(11);err != nil {
// t.Log(err)
// t.Fail()
//}
//if err := tree.Delete(9);err != nil {
// t.Log(err)
// t.Fail()
//}
if err := tree.Delete(5);err != nil {
t.Log(err)
t.Fail()
}
if err := tree.Delete(6);err != nil {
t.Log(err)
t.Fail()
}
if err := tree.Delete(2);err != nil {
t.Log(err)
t.Fail()
}
if err := tree.Delete(12);err != nil {
t.Log(err)
t.Fail()
}
PrintTree(tree.root, 0, "root", 10)
_, err := tree.Search(11)
if err == nil {
t.Log(err)
t.Fail()
}
}
func BenchmarkRedBlackTree_Search(b *testing.B) {
b.ResetTimer()
for i := 0; i < b.N; i++ {
tree := NewRedBlackTree()
for i := 0; i < 1000; i++ {
//fmt.Print(i, ",")
tree = tree.Insert(NewRedBlackTreeNode(i))
}
for i := 0; i < 100000; i++ {
_, err := tree.Search(rand.Intn(999))
if err != nil {
b.Log(err)
b.Fail()
}
}
}
}
好好学习,天天向上